제어 평면이란 네트워크 전체를 아우르는 구성요소로서, 데이터그램이 출발지 호스트로부터 목적지 호스트까지의 경로를 따라 어떻게 전달되어야 하는지뿐만 아니라 네트워크 계층 구성요소와 서비스를 어떻게 설정하고 관리할지도 제어한다.
라우팅 알고리즘
라우팅 알고리즘(routing algorithm)의 목표는 송신자부터 수신자까지 라우터의 네트워크를 통과하는 좋은 경로를 결정하는 것이다. 일반적으로 '좋은' 경로란 최소 비용 경로를 말한다.
라우팅 알고리즘의 분류
중앙 집중형 vs 분산형
- 중앙 집중형 라우팅 알고리즘(centralized routing algorithm)
- 네트워크 전체에 대한 완전한 정보를 가지고 출발지와 목적지 사이의 최소 비용 경로를 계산한다.
- 링크 상태(link-state, LS) 알고리즘
- 분산 라우팅 알고리즘(decentralized routing algorithm)
- 최소 비용 경로의 계산이 라우터들에 의해 반복적이고 분산된 방식으로 수행
- 어떤 노드도 모든 링크의 비용에 대한 완전항 정보를 가지고 있지 않음
- 각 노드는 자신에게 직접 연결된 링크에 대한 비용 정보만을 가지고 경로 계산을 시작한다.
- 거리 벡터(distance-vector, DV) 알고리즘
정적 알고리즘 vs 동적 알고리즘
- 정적 라우팅 알고리즘 : 경로가 느리게 변한다.
- 동적 라우팅 알고리즘 : 네트워크 변화에 빠르게 대응한다.
부하에 민감한지에 따른 분류
- 부하에 민감한 알고리즘 : 링크 비용은 해당 링크의 현재 혼잡 수준을 나타내기 위해 동적으로 변한다.
- 부하에 민감하지 않은 알고리즘
- 링크 비용이 현재의 혼잡을 반영하지 않음
- RIP, OSPF, BGP
링크 상태(LS) 라우팅 알고리즘
모든 노드가 링크 비용을 알고 있음(중앙 집중형)
- 모든 노드가 동일한 정보를 가지고 있다.
링크 상태 알고리즘은 다익스트라 알고리즘(Dijkstra's algorithm)이다.

- 초기화
- u와 인접한 노드 v의 경로가 있으면 D(v)값을 설정한다.
- 없으면 무한대로 설정한다.
- 반복
- N'에 포함되지 않으며 가장 최소의 값 D(w)를 가지는 w를 N'에 넣는다.
- N'에 포함되지 않으면서 w와 인접한 모든 노드들의 거리 D(v)값을 계산한다.
- D(v)는 기존 D(v)의 값과 새로 계산된 값 중 작은 값으로 설정된다.
- 반복은 N'에 모든 노드가 포함될 때 까지 계속해서 반복한다.
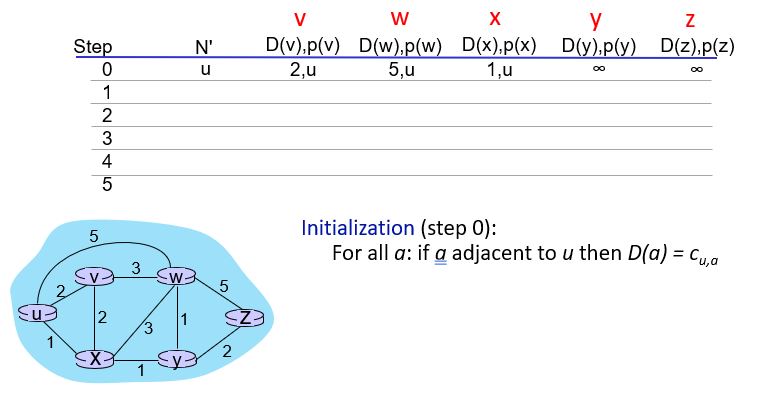
u와 인접하면 값을 설정하고 없으면 무한대로 설정한다.
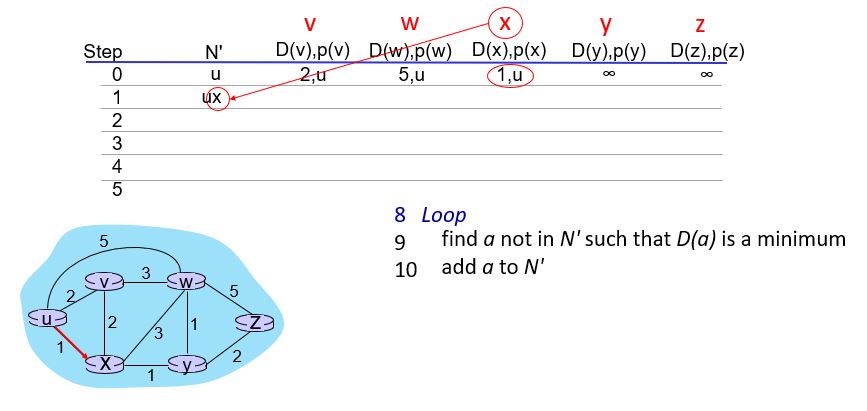
D(x)의 값이 1로 제일 작다. 따라서 N'에 D(x)를 포함한다.

x로부터 인접한 모든 D(b)의 값을 계산한다.
이를 계속해서 반복하면 다음과 같은 결과가 나온다.
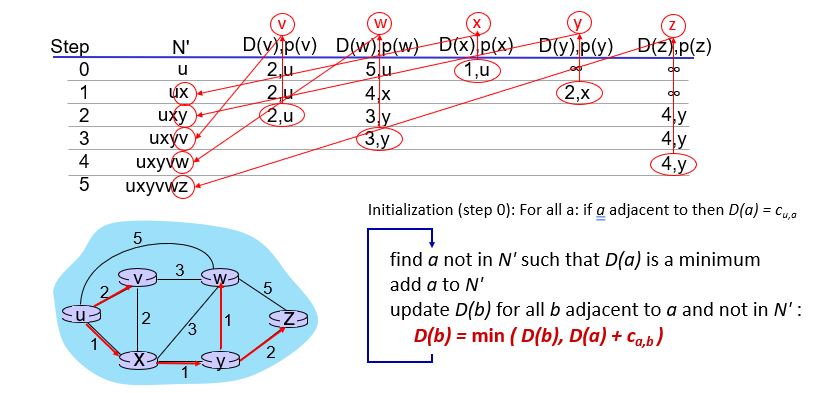
거리 벡터(DV) 라우팅 알고리즘
링크 상태 알고리즘이 네트워크 전체 정보를 이용하는 알고리즘인 반면에, 거리 벡터(distnace-vector, DV)알고리즘은 반복적이고 비동기적이며 분산적이다.
- 각 노드는 하나 이상의 직접 연결된 이웃으로부터 정보를 받고, 계산을 수행하며, 계산된 결과를 다시 이웃에게 배포한다.
- 이웃끼리 더 이상 정보를 교환하지 않을 때까지 프로세스가 지속된다.
거리 벡터 알고리즘은 벨만-포드(Bellman-Ford)식(equation)에 기반한다.
Dx(y) = MINv{c(x,v) + Dv(y)}예를 들어 Du(z)는 c(u,v) + Dv(z), c(u,w) + Dw(z), c(u,x) + Dx(z)에서 최솟값을 선택한다.
거리벡터 알고리즘(DV)
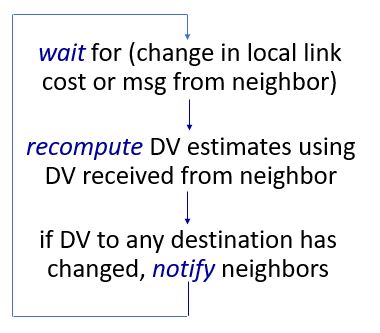
- 특정 노드가 자신에게 직접 연결된 링크 중 하나의 비용이 변경된 사실을 알게 되거나, 어떤 이웃으로부터 변경된 거리벡터를 수신했을 때 자신의 거리 벡터 추정값을 갱신한다.
- 거리 벡터 값이 변경되면 이웃에게 이 사실을 알린다.
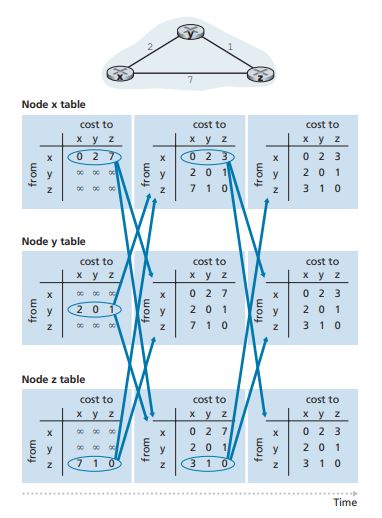
좌측에서 우측순으로 진행된다. 첫 번째 시점에 각 노드 테이블은 값을 세팅하고 이웃 노드에게 변경된 값을 전달한다. 변경된 값을 이용해서 from, to의 값을 결정한다.
예를 들어 두 번째 시점에서 x 테이블의 값은 다음과 같이 계산 된다.
Dx(x) = 0
Dx(y) = min{c(x,y) + Dy(y), c(x,z) + Dz(y)} = min{2 + 0, 7 + 1} = 2
Dx(z) = min{c(x,y) + Dy(z), c(x,z) + Dz(z)} = min{2 + 1, 7 + 0} = 3두 번째 시점에 노드 y 테이블은 변경 사항이 없으므로, 세 번째 시점에 이웃에게 변경된 값을 전달하지 않는다. 노드 x 테이블과 노드 z 테이블은 변경된 값을 이웃에게 전달한다.
이러한 과정을 모든 테이블이 정보를 교환하지 않을 때 까지 진행한다.
거리 벡터(DV) 알고리즘: 링크 비용 변경과 링크 고장
링크 비용이 감소하는 경우
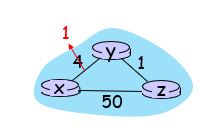
- t0 시점에 y가 링크 비용의 변화(4 -> 1)를 감지하고, 자신의 거리 벡터를 갱신한 후 이웃에게 알린다.
- t1 시점에 z는 y로 부터 갱신 정보를 받고 z에서 x까지의 거리를 2로 변경하고, 자신의 새로운 거리 벡터를 이웃에게 알린다
- t2 시점에 y는 z로부터 갱신 정보를 받고 자신의 테이블을 갱신한다. y의 최소 비용은 변화가 없으므로 갱신을 하지 않고, y는 z에게 아무런 메시지를 보내지 않는다.
링크 비용이 증가하는 경우
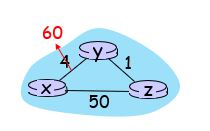
- Dy(x) = min(c(y,x) + Dx(x), c(y,z) + Dz(x)) = min{60+0, 1+5} = 6이 된다.
- y는 x로 가기 위해, y->z, z->y로 경로를 설정하는 라우팅 루프(routing loop)가 발생한다.
- x를 목적지로 하는 패킷이 y나 z에 도착하면 이 두노드 사이에 영원히(또는 포워딩 테이블이 변할 때 까지) 순환할 것이다.
- Dz(x)는 7,8,9... 이런 식으로 증가하게 된다.
거리 벡터 알고리즘: 포이즌 리버스 추가
z가 y를 통해 목적지 x로 가는 경로를 설정했다면, z는 y에게 x까지의 거리가 무한대라고 알리면 된다.
z는 y를 통과해서 x로 가는 동안은 이러한 선의의 거짓말을 계속 한다.
- y는 z에서 x로 가는 경로가 없다고 믿으므로, z가 계속해서 y를 통해 x로 가는 경로를 사용하는 동안은 y는 z를 통해 x로 가는 경로를 시작하지 않을 것이다.
비용이 증가하는 경우 설명
- 포이즌 리버스로 인해 Dz(x) = 무한 값을 갖는다.
- Dy(x) = 60로 설정하고 이를 z에게 알린다. z는 Dz(x)= 50이 되고, 이를 y에게 알린다.
- y는 Dy(x) = 51로 갱신한다. 그리고 z에게는 Dy(x) = 무한 으로 알린다.(z에서 x로의 역경로 차단)
위의 경우는 해결이 되었지만, 3개 이상의 노드를 포함한 루프는 포이즌 리버스로 감지할 수 없다.
'네트워크' 카테고리의 다른 글
| 링크 계층 소개 (3) | 2024.04.01 |
|---|---|
| 인터넷에서의 AS 내부 라우팅: OSPF (4) | 2024.03.12 |
| 인터넷 프로토콜(IP) : IPv4, 주소체계, IPv6 (2) | 2024.03.04 |
| 네트워크 계층 개요 (3) | 2024.02.23 |
| 혼잡 제어 (3) | 2024.02.19 |



